


Next: References
Up: No Title
Previous: No Title
An observed time series of photon counts,
fobs(t), which is binned
into time intervals of length  ,
so that the number
,
so that the number
![$n_i=f^{obs}[t_i < t <t_i+\Delta t]$](img3.gif) represents the photon counts
in bin
represents the photon counts
in bin
![$[t_i,t_i+\Delta t]$](img4.gif) ,
is modeled by an analytical function,
fmodel(t), which predicts an expectation value
,
is modeled by an analytical function,
fmodel(t), which predicts an expectation value
![$e_i=f^{model}[t_i < t <t_i+\Delta t]$](img5.gif) of photon counts in time bin i.
In the limit of large-number counts,
of photon counts in time bin i.
In the limit of large-number counts, 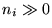 ,
Poisson statistics
can be approximated by a Gaussian distribution, which predicts an
r.m.s. noise of
,
Poisson statistics
can be approximated by a Gaussian distribution, which predicts an
r.m.s. noise of
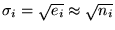 .
The goodness of fit of a model can then be evaluated by the well-known
.
The goodness of fit of a model can then be evaluated by the well-known
 -statistic,
-statistic,
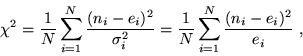 |
(1) |
yielding a normalized value of
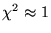 in the case when
the model is consistent with the data, within the uncertainties of the
expected noise.
in the case when
the model is consistent with the data, within the uncertainties of the
expected noise.
For sparse sampling, in particular when the observed time series nicontains zeroes or few counts, say
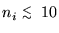 ,
e.g. as it is the
case for the modulation profiles of the finest HESSI collimators, where the
total photon counts are binned into some
212=4096 time bins to resolve the
rotational modulation, the Gaussian
,
e.g. as it is the
case for the modulation profiles of the finest HESSI collimators, where the
total photon counts are binned into some
212=4096 time bins to resolve the
rotational modulation, the Gaussian 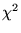 -statistic is not appropriate
anymore. Photon counting statistics for sparse sampling can be derived from
the general probability function P as outlined by Cash(1979), which is
-statistic is not appropriate
anymore. Photon counting statistics for sparse sampling can be derived from
the general probability function P as outlined by Cash(1979), which is
 |
(2) |
for a particular result ni given the correct set of ei. The likelihood
radio, called C-statistic by Cash (1979), can be expressed in logarithmic
form from Eq.A2,
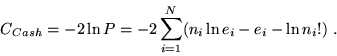 |
(3) |
Let the theoretical model
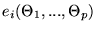 be
defined by p free parameters
be
defined by p free parameters
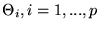 .
The
best-fitting model is found by varying all p parameters
.
The
best-fitting model is found by varying all p parameters
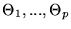 until the C-statistic reaches a minimum, which we
denote by
(Cmin)p. Now, during the iterative fitting procedure,
only a partial subset of model parameters, say q parameters (with q
< p), may have already converged to the true solution,
until the C-statistic reaches a minimum, which we
denote by
(Cmin)p. Now, during the iterative fitting procedure,
only a partial subset of model parameters, say q parameters (with q
< p), may have already converged to the true solution,
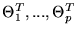 ,
so that
,
so that
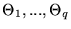 are set to
are set to
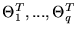 ,
while the remaining p-qparameters,
,
while the remaining p-qparameters,
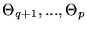 ,
still need to be
varied until a global minimum of C is reached. We denote this
partial solution, where p-q parameters have already converged to the
true solution
,
still need to be
varied until a global minimum of C is reached. We denote this
partial solution, where p-q parameters have already converged to the
true solution
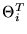 ,
with the value
(Cmin)Tp-q.
According to the theorem of Wilks (1938; 1963), the difference,
,
with the value
(Cmin)Tp-q.
According to the theorem of Wilks (1938; 1963), the difference,
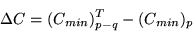 |
(4) |
will be distributed as 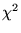 with q degrees of
freedom. Therefore, the quantity
with q degrees of
freedom. Therefore, the quantity 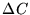 can be used to establish a
confidence criterion of the model ei to the data ni. Following
Cash (1979), the term
can be used to establish a
confidence criterion of the model ei to the data ni. Following
Cash (1979), the term 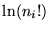 of Eq.A3 drops out in the difference
of Eq.A3 drops out in the difference
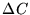 ,
because only the parameters
,
because only the parameters
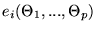 are varied during the fitting procedure. Thus, it is more
convenient to use the simplified statistic
are varied during the fitting procedure. Thus, it is more
convenient to use the simplified statistic
 |
(5) |
For the evaluation of the difference 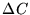 in Eq.A4 we have the
partially optimized term
(Cmin)Tp-q,
in Eq.A4 we have the
partially optimized term
(Cmin)Tp-q,
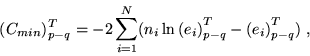 |
(6) |
and the absolute minimum
(Cmin)p, which represents the asymptotic limit
when the data ni perfectly match the model, i.e. ei=ni,
![\begin{displaymath}(C_{min})_p = - 2 \sum_{i=1}^N [n_i \ln (n_i) - n_i ] \ .
\end{displaymath}](img26.gif) |
(7) |
The combination of Eq.A4-A6 yields then
![\begin{displaymath}\Delta C = - 2 \sum_{i=1}^N [n_i \ln (e_i) - e_i - n_i \ln
(n_i) + n_i] \ .
\end{displaymath}](img27.gif) |
(8) |
Instead of the reduced 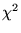 -statistic (A1), we can therefore use
the equally-simple
-statistic (A1), we can therefore use
the equally-simple
C-statistic (where we drop the symbol 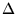 for brevity),
for brevity),
![\begin{displaymath}C := {1 \over N}\Delta C = {2 \over N} \sum_{i=1}^N [n_i \ln
({n_i \over e_i}) - (n_i - e_i)] \ .
\end{displaymath}](img29.gif) |
(9) |
This form has the advantage that, in addition to being asymptotic to
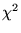 ,
C vanishes identically when the model fits the data exactly.
Numerical care has to be taken for the time bins that contain zeroes
in the data, ni=0, in which case the mathematical relation
,
C vanishes identically when the model fits the data exactly.
Numerical care has to be taken for the time bins that contain zeroes
in the data, ni=0, in which case the mathematical relation
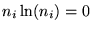 has to be used to avoid the singularity
has to be used to avoid the singularity
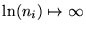 .
On the other side, a singularity could arise when the model
predicts zero counts, ei=0, but the observed counts are not zero,
.
On the other side, a singularity could arise when the model
predicts zero counts, ei=0, but the observed counts are not zero,
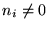 ,
because the term
,
because the term
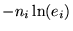 yields than
infinity. It seems therefore to be recommendable to restrict the model
fit to time intervals with a finite probability for photon counts,
i.e. ei>0.
yields than
infinity. It seems therefore to be recommendable to restrict the model
fit to time intervals with a finite probability for photon counts,
i.e. ei>0.



Next: References
Up: No Title
Previous: No Title
Ed Schmahl
1999-12-17
![]() ,
so that the number
,
so that the number
![]() represents the photon counts
in bin
represents the photon counts
in bin
![]() ,
is modeled by an analytical function,
fmodel(t), which predicts an expectation value
,
is modeled by an analytical function,
fmodel(t), which predicts an expectation value
![]() of photon counts in time bin i.
In the limit of large-number counts,
of photon counts in time bin i.
In the limit of large-number counts, ![]() ,
Poisson statistics
can be approximated by a Gaussian distribution, which predicts an
r.m.s. noise of
,
Poisson statistics
can be approximated by a Gaussian distribution, which predicts an
r.m.s. noise of
![]() .
The goodness of fit of a model can then be evaluated by the well-known
.
The goodness of fit of a model can then be evaluated by the well-known
![]() -statistic,
-statistic,
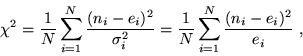
![]() ,
e.g. as it is the
case for the modulation profiles of the finest HESSI collimators, where the
total photon counts are binned into some
212=4096 time bins to resolve the
rotational modulation, the Gaussian
,
e.g. as it is the
case for the modulation profiles of the finest HESSI collimators, where the
total photon counts are binned into some
212=4096 time bins to resolve the
rotational modulation, the Gaussian ![]() -statistic is not appropriate
anymore. Photon counting statistics for sparse sampling can be derived from
the general probability function P as outlined by Cash(1979), which is
-statistic is not appropriate
anymore. Photon counting statistics for sparse sampling can be derived from
the general probability function P as outlined by Cash(1979), which is

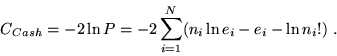

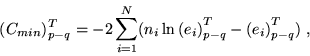
![\begin{displaymath}(C_{min})_p = - 2 \sum_{i=1}^N [n_i \ln (n_i) - n_i ] \ .
\end{displaymath}](img26.gif)
![\begin{displaymath}\Delta C = - 2 \sum_{i=1}^N [n_i \ln (e_i) - e_i - n_i \ln
(n_i) + n_i] \ .
\end{displaymath}](img27.gif)
![]() for brevity),
for brevity),
![\begin{displaymath}C := {1 \over N}\Delta C = {2 \over N} \sum_{i=1}^N [n_i \ln
({n_i \over e_i}) - (n_i - e_i)] \ .
\end{displaymath}](img29.gif)