Bayesian justification for MEM --- The Maximum Entropy Method

• The ``Maximum Entropy Method'' is a common and powerful technique
• For deconvolving sidelobes
• Or solving indeterminate systems
• Often justified as an ad hoc balance between goodness-of-fit and simplicity
• Actually can be derived using Bayesian methods

The Bayesian probabilistic method

• The Bayesian probabilistic method uses two basic concepts:
  • "prior probability"
  • "likelihood"
• Functions of the intensities
• and the observables
• The probability of an image is the product of the ``prior'' and the ``likelihood''
• This product has a maximum value for some particular map,
• which is usually called the MEM map.

The ``prior probability'' $P(b)$ represents the chance that the image b represents the true map before any data is taken into account. This ``prior probability'' is a measure of how simple an image is, since simple images are more probable (a priori) than complex images.

The Prior Probability

How do we get the "prior probability" $P(b)$?   A monkey argument was suggested by Gull and Daniell (1978).

Suppose a monkey tosses N identical photons into M identical pixels: (The order of the pixels in image $b=\{b_1,b_2,...,b_M\}$ is regarded as irrelevant, and the photons are identical.

    Number of photons in jth pixel = $b_j$

    Number of ways to get a given image $\{b_j \vert j=1,...,M\}$

$$= {{N!} \over {b_1! b_2! \cdots b_M!}}$$ (1)

The a priori probability of getting a given image b is therefore this number divided by the number of all possible maps:

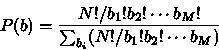$$P(b) = {{N!/b_1! b_2! \cdots b_M!} \over {\sum_{b_i}(N!/b_1! b_2! \cdots b_M)} }$$ (2)

If there are many photons in each pixel ($b_i >> 1$) we can use Stirling's approximation for the factorial, $b_i! \approx (b_i/e)^{b_i}$. Using this, $P(b) \propto b_1^{b_1} b_2^{b_2} \cdots b_M^{b_M}$.

It is much more convenient to normalize all the pixel intensities $b_i$ to the so-called ``grey map'', where all the intensities equal the mean value $\bar{b} = N/M$.

$$P(b) = {{P_G} \over {(b_1/\bar{b})^{b_1} (b_2/\bar{b})^{b_2} \cdots(b_M/\bar{b})^{b_M}}},$$ (3)

where $P_G$ is a normalizing constant that guarantees that $P(b)$ sums to 1 over all possible maps $f$. $P_G$ is the probability of the ``grey'' map, since all the factors $(b_j/\bar{b})$ in equation (3) are 1 in that case. It can be shown that $P_G$ is the maximum value of $P(b)$.

None of this looks at all like the ``entropy'' term we are familiar with in MEM, but equation (3) can be re-written in an exponential form which gives us the so-called ``entropy'' term $S=-\sum_i{b_i log(b_i/\bar{b})}$.

$$P(b) = e^{-\alpha{\sum_i{b_i log(b_i/\bar{b})} }}$$ (4)

In our derivation,

The Likelihood

Now that we have the ``prior'' probability, we need to find the "likelihood". The "likelihood" $P(D \vert b)$ (``P of D given b'') is the probability that the observed data D could have been generated from a given image b. )

This probability is computed using the difference of the simulated data $D_{sim}$ computed from some guess for the image b and the real data D. For Gaussian statistics,

$$P(D \vert b) \sim e^{-{1 \over 2}(D-D_{sim})^2/\sigma^2}$$ (5)

In somewhat more generality,

$$P(D \vert b) \sim e^{-{1 \over 2}\chi^2}$$ (6)

This is true for a sufficiently large number of photons that $\chi^2$ is a valid measure of departures from data. If the number of photons is small, one must use something like the C-statistic (Cash, 1978).

But what we want for the deconvolution is not $P(D \vert b)$ but $P(b \vert D)$, that is, the probability of the image b given the data D. This is given by Bayse's theorem:

$$P(b \vert D) = P(b) * P(D \vert b)/P(D)$$ (7)

P(b) is the prior probability of image b, $P(D \vert b)$ is the likelihood of the data given b, and P(D) is a constant which normalizes $P(b \vert D)$ to a sum of unity, and gives the probability of the data.

At last we can write down the quantity to be maximized. Inserting the expressions (2) and (4) for $P(b)$ and $P(D \vert b)$ into equation (5), we get:

$$P(b \vert D) = C e^{-{1 \over 2}\chi^2} \times e^{-\alpha \sum b_i log(b_i/\bar{b})}$$ (8)

where C is a normalizing constant that guarantees that the sum of the probabilities is 1. All we need to do now is find the image b that maximizes $P(b\vert D$), which is the same as maximizing $log(P(b\vert D)$:

$$log(P(b\vert D)) = -{1 \over 2}\chi^2 - \alpha \sum b_i log(b_i/\bar{b})$$ (9)

The first term is the constraint of the data; it is 0 when the image matches the data perfectly, but in realistic cases is $\sim 1$ when the data are fitted but not ``over fitted''. The second term is commonly called the "entropy" term, which guarantees the "simplicity" of the image. (It is not really the entropy in the sense used by Shannon (1948), but the weight of common use forces us to call it that.) The ``entropy'' term is maximum (0) when $b_i = \bar{b}$. That is, the ``grey'' map is a priori most probable.

Note the arbitrary coefficient $\alpha$ giving relative weight to the ``entropy'' term. If $\alpha=1$, Bayesian logic would give equal weight to each term, but MEM algorithms usually weight them differently to provide simpler maps ($\alpha > 1$) or maps more faithful to the data ($\alpha < 1$). It is possible, using Bayseian arguments, to estimate the most probable $\alpha$ (Skilling 1989)

Example of a simple MEM problem

Since the dimensionality of the parameter space for MEM is the number of map pixels, we cannot show contours of the function $P(b\vert D$) in a realistic case. Instead we show a case for 3 pixels, {$b_1,b_2,b_3$}, where the sum of the pixel brightnesses equals 100. This reduces it to a 2-dimensional problem. In the figure below, the dashed contours represent the entropy function $S(b)$, and the solid contours show the $\chi^2$ function. The squares are located at the maximum of $P(b\vert D)$ for different values of $\alpha$. When $\alpha=\infty$, the maximum is located at the entropy peak, and when $\alpha=0$, it is located at the minimum of $\chi^2$.

This figure shows a cross-section through the (3-D) likelihood hypercube. In general, the likelihood hypercube will have a number of dimensions equal to the number of map pixels (e.g. 4096 for a 64x64 map). This 3-pixel example is more general than one might at first think. In fact, for an arbitrary number of pixels, any two-dimensional cross section of the N-dimensional entropy function through parameter space will look much like this. The cross-sections of the $\chi^2$ function will always be ellipses with, of course, different centroids and axial ratios.

There is a special high-noise case in which the $\chi^2$ = 1 surface is outside the entropy=0 point. This happens when the sigmas are larger than the distance from the entropy=0 point to the $\chi^2$ = 0 point. For example:

In this case, the track given by alpha=infinity to zero does not cross the surface $\chi^2$ = 1 at the point of maximum entropy (marked by the "bulls eye".) This may never happen with RHESSI data, but it is worth investigating.

The goal of MEM is to find the optimum value along this curve, somewhere in parameter space between the "prior" grey map and the map which fits the data exactly. Skilling has argued that the ``most probable'' $\alpha$ is the one that makes the number of ``good'' measurements equal to -$2 \alpha S(b)$, which is the (dimensionless) amount of structure in the map $f$. The number of ``good'' measurements is defined by a sum over curvature terms in the likelihood matrix (Skilling 1989).

To Using MEM Sato