Solar Aspect System SAS

Figure 1: The aspect coordinate system. The circle drawn with a solid line represents the Solar limb. (x,y) refers to an inertial coordinate system with y pointing towards the north celestial pole. (x,y) refers to the imaging coordinate system, which is fixed to the S/C. P is the pointing vector in units of [arcsec] and $\varphi$ is the rotation angle in [radian], which is increasing in time.

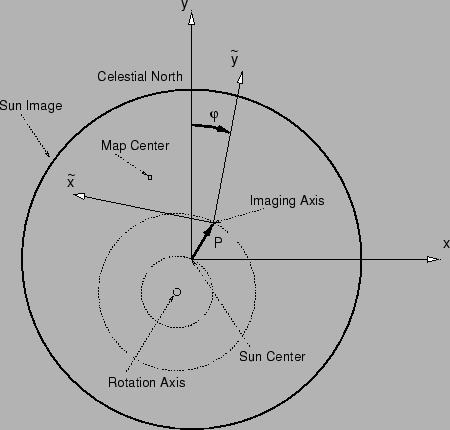
The SAS features define the reference coordinate system to be used for the image reconstruction. This coordinate system is called the imaging coordinate system (or SAS coordinate system) and has been chosen in order to optimize the SAS field of view in a symmetrical way. The z-axis is parallel to the line from the center of gravity of the three CCD mid-points to the center of gravity of the lens centers and its pointing towards the Sun. The x- and y-axis are chosen to form a right-handed Cartesian coordinate system with the y-axis being parallel to the xy-plane of the rear tray coordinate system, which had been used as the reference for building the imager. The origin of the imaging coordinate system is the center of gravity of the CCD mid-points.

In Fig. 1 x and y refers to the SAS coordinate system. In spacecraft fixed coordinates, the pointing is given by the vector from the origin of the SAS coordinate system to the momentary Sun center and is measured as an angle in arcsec. Therefore, the pointing is the x- and y-component of the angle between the z-axis and the direction towards the Sun center. Internally of the aspect solution software, the limb positions are calculated in a pixel based coordinate system. Using the appropriate plate scale, the coordinates are converted to arcsec in order to provide a SAS solution.