Determining Coefficients in Fourier Series

Since we are most interested in Fourier series on discrete sets, where the independent variable t assumes only values which are equally spaced, it is possible to simplify the more general problem (which involves integration) and restrict ourselves to finite sums. It turns out to be very convenient to use the complex form of the trig functions:

$$e^{2i\pi x} = cos(2\pi x) + i\ sin(2\pi x)$$

The standard programs for computing Fourier series almost always use the complex types for variables, so this is not a computational complication. Going to the complex plane, we look for the coefficients c_k in the Fourier expansion of an arbitrary function f(t) at 2N+1 equally-spaced points on the interval $(-N \le t \le N)$:

$$f(t)=\sum_{k=-N}^N c_k e^{2\pi i k t/(2N+1)}, t=-N,\cdots,N \eqno{(1)}$$

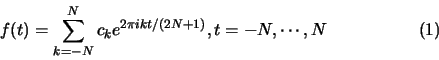
The right hand side of this equation has 2N+1 coefficients c_k, which are to be determined, and we assume that f(t) is known at 2N + 1 points on the range $-1 \le t \le 1$. Let's look at an example with N=1 and t=[-1.,0,1.]:

$$f(-1)=c_{-1}e^{+2\pi i/3}\ +\ c_0 \ +\ c_{1}e^{-2\pi i/3}$$

$$f(0)=c_{-1}\qquad\qquad +\ c_0 \qquad +\ c_{1}$$

$$f(1)=c_{-1}e^{-2\pi i/3}\ +\ c_0 \ +\ c_{1}e^{+2\pi i/3}$$

There are 2N+1 independent equations in 2N+1 (complex) unknowns, and the system is therefore invertible by matrix methods. In IDL one could create a matrix M and find the solution c_k using the invert command:

IDL> N=1 & t=[-1.,0,1.] & N1N=2*N+1.

IDL> i=complex(0,1)

IDL> M=[ [ exp(-2*!pi*i*t(0)/N1N),1., exp(2*!pi*i*t(0)/N1N)], $

IDL> [ exp(-2*!pi*i*t(1)/N1N),1., exp(2*!pi*i*t(1)/N1N)], $

IDL> [ exp(-2*!pi*i*t(2)/N1N),1., exp(2*!pi*i*t(2)/N1N)] ]

IDL> M_invert = invert(M)

But it turns out that the inverse of the matrix M is simply (1/(2N+1) times its complex conjugate, obtained by reversing the sign of i in all the terms. Compare the two matrices term by term to verify this. So the solution to the problem of finding the c coefficients is:

IDL> M_invert = conj(M)/(2*N+1) ; Simpler form of the inverse

IDL> f=randomn(seed,3) ; any random array of values

IDL> print,f

IDL> c=M_invert ## f

IDL> print,c

IDL> ff=M ## c ; return to the original array f

IDL> print,ff ; compare with f

Exercise:

Try creating a larger array f and find the coefficients c using the above recipe with M and its inverse. Then compute M## c as above and see if it is the same as f.