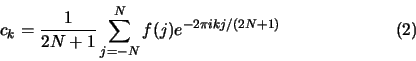
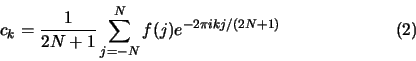
Equation (1) is the so-called forward transform and equation (2) is the inverse transform. We can show that (2) is valid by substituting the right hand side of (2) where ck appears in (1):
![\begin{displaymath}f(t)=\sum_{k=-N}^N \Bigl[ {1 \over {2N+1}}\sum_{j=-N}^N f(j) e^{-2\pi i kj/(2N+1)} \Bigr] e^{2\pi i k t/(2N+1)} \end{displaymath}](img10.gif)
Then change the order of the sums, and simplify, getting:
![\begin{displaymath}f(t)= {1 \over {2N+1}} \sum_{j=-N}^N f(j) \Big[ \sum_{k=-N}^N e^{2\pi i k(t-j)/(2N+1)}\Bigr] \eqno{(3)} \end{displaymath}](img11.gif)
It turns out that the sum over k inside the big brackets vanishes except when
t=j. This miraculous result is the secret mechanism inside Fourier transforms,
and the reason it works is most easily understood
geometrically. All of the terms
![]() are ``phasors''.
That is, they are unit vectors with a phase angle
are ``phasors''.
That is, they are unit vectors with a phase angle
![]() measured counter clockwise from the x axis. The phasors always occur
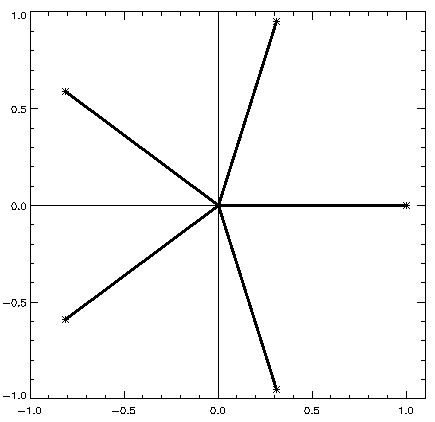
in regular arrays. Thus, when N=2, we have 5 phasors:
measured counter clockwise from the x axis. The phasors always occur
in regular arrays. Thus, when N=2, we have 5 phasors:
|
consisting of vectors pointing away from the origin at angles 72° with respect to one another. Their end points form a regular pentagon about the origin. Because of this symmetry, the sum of the phasors is equal to zero, and the same is true for any N. In equation (3), as long as the quantity (t-j) is non zero, the sum will be over N symmetrically-arranged phasors, and they will add to zero. When (t-j) is zero, the sum over k is 2N+1, and equation (3) reduces to f(t)=f(t). |
Exercise:
Write an IDL program that plots the phasors in equation (3) for general N and for all t and j. Verify geometrically that the phasors are all symmetrically arranged around the origin.